|
(4.0) 1) |
Considere o planeta Terra como uma esfera
homogénea de densidade 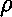 =3MT/(4
=3MT/(4 RT3)=
5.5 x 103 kg/m3
(desprezando a atmosfera). RT3)=
5.5 x 103 kg/m3
(desprezando a atmosfera).
(2.0) a) Qual a força sentida por uma massa de 1 kg, e o valor
da sua Energia Potencial (admitindo que infinitamente longe esta seria nula),
em função da distância ao centro, r?
Possível resolução:
A Força é o produto do campo gravítico pela massa. Assim a força
sentida por uma massa de 1 kg, é igual ao valor do campo gravítico
(com o mesmo sentido). O campo gravítico tem a direcção
radial, e aponta para o centro da Terra.
O valor do Campo gravítico G= Ger (G<0)
pode calcular-se usando o Teorema de Gauss:
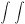 G.n dS =
- 4 G.n dS =
- 4 GNMint GNMint
Escolhendo uma superfície esférica concêntrica com a Terra,
de raio r em que o campo é constante e anti-paralelo à normal
à superfície, o integral ao longo dessa superfície tem
o valor
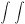 G.n dS
= 4 G.n dS
= 4 r2 G =
(T.Gauss)= - 4 r2 G =
(T.Gauss)= - 4 GNMint <=>
G = - GN/r2 Mint <=> GNMint <=>
G = - GN/r2 Mint <=>
|
0 <= r < RT : |
Mint =
(4/3) r3 r3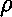 =
r3 MT/(RT3) =
r3 MT/(RT3) | <=> |
G = - GN MT/(RT3) r | |
r > RT : |
Mint = MT | <=> | G = -GN MT/r2
|
Para calcular a energia potencial, usamos as expressões
EP = m VG = -m 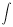 G.dr G.dr
para as duas regiões diferentes. Resolvendo os integrais indefinidos, ficam duas constantes a determinar pela condição
fronteira VG(r = 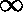 ) = 0, e pela necessidade de continuidade
do potencial para r = RT. ) = 0, e pela necessidade de continuidade
do potencial para r = RT.
Assim, temos:
|
r > RT : |
- 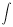 G.dr =
- GN MT/r + Cte = - GN MT/r
(pois VG(r = G.dr =
- GN MT/r + Cte = - GN MT/r
(pois VG(r = 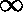 ) = 0) ) = 0)
| => VG(r = RT) = - GN MT/RT |
|
0 <= r < RT : |
- 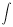 G.dr =
- GN MT/(RT3 ) r2/2 +Cte G.dr =
- GN MT/(RT3 ) r2/2 +Cte
e VG(r = RT) = - GN MT/RT |
=> VG = - GN MT/(RT3 )
r2/2
- GN MT/(2 RT) | |
(1.0) b) Se a massa da Terra estivesse distribuída em camadas homogéneas,
de densidades respectivamente iguais a
|
0 | <= | r < 4 x 106m |
 |
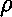 = =
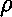 1 =
Cte = 1.5 x 104 kg/m3 1 =
Cte = 1.5 x 104 kg/m3
| |
4 x 106m | <= | r < 6 x 106m |
 |
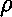 = =
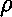 2 =
Cte = 2.8 x 103 kg/m3 2 =
Cte = 2.8 x 103 kg/m3
| |
6 x 106m | <= | r < RT |
 |
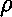 = =
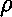 3 =
Cte = 9.4 x 102 kg/m3 3 =
Cte = 9.4 x 102 kg/m3
|
qual seria o valor do campo gravítico em função da distância
ao centro da Terra (módulo, direcção e sentido)?
Possível Resolução:
A direcção e sentido de G seria sempre radial e apontando para o centro da Terra,
Gi=-Gi(r ) er. Mas agora há
que separar as diferentes regiões:
| 1: |
0 <= r < 4 x 106 m: |
- G1 . 4 r2 =
- 4 r2 =
- 4 GN(4 GN(4 /3) /3)
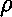 1r3 1r3 | <=> |
G1 = - 4.19 x 10-6 r (m/s2)
|
| 2: |
4 x 106 m <= r < 6 x 106 m: |
- G2 . 4 r2 =
- 4 r2 =
- 4 GN Mint =
- 4 GN Mint =
- 4 GN (M1 + GN (M1 +
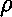 2 . Vol2(r ) ) = 2 . Vol2(r ) ) = | | |
|
- 4 GN
[(4 GN
[(4 /3) . (4 x 106)3 .
( /3) . (4 x 106)3 .
(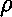 1 - 1 - 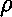 2) + 2) +
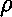 2 .
(4 2 .
(4 /3) r3 ) ] <=> /3) r3 ) ] <=>
| | | |
G2 = - 2.18 x 1014/r2 - 7.83 x 10-7 r (m/s2)
|
| 3: |
6 x 106 m <= r < RT : |
- G3 . 4 r2 =
- 4 r2 =
- 4 GN (M1 + M2 + GN (M1 + M2 +
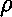 3 . Vol3(r ) ) = 3 . Vol3(r ) ) = | | |
|
- 4 GN
[(4 GN
[(4 /3) . (4 x 106)3 .
( /3) . (4 x 106)3 .
(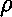 1 - 1 - 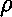 2) +
(4 2) +
(4 /3) . (6 x 106)3 .
( /3) . (6 x 106)3 .
(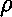 2 - 2 - 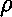 3) + 3) +
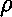 3 .
(4 3 .
(4 /3) r3 ) ] /3) r3 ) ]
| | | |
<=>
G3 = - 3.31 x 1014/r2 - 2.63 x 10-7 r (m/s2)
|
| 4: |
r > RT ( = 6.376 x 106 m) : |
- G4 . 4 r2 =
- 4 r2 =
- 4 GN Mint GN Mint | <=> |
G4 = - 3.98 x 1014 / r2 (m/s2) |
(1.0) c) Nas condições do problema anterior, qual seria a energia potencial
de uma massa de 1 kg em função da distância ao centro
(admitindo que seria nula infinitamente longe da Terra)?
Possível Resolução:
Nas 4 regiões, VG obtém-se de
Vi = - 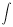 G.dr + Ci G.dr + Ci
em que Ci são constantes a determinar pelas condições fronteira, e a Energia potencial para uma massa de 1 kg
obtém-se de
EP = m Vi = (1 kg.)Vi.
As condições fronteira resumem-se ą necessidade de continuidade da função potencial, e ao dito no enunciado que
V(r -> 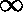 ) = 0. ) = 0.
Comecemos então pela região 4, para utilizar este dado inicial:
V4 = - 3.98 x 1014 /r + C4 = - 3.98 x 1014 /r (J/kg)
(C44 = 0 quando r = 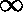 ) )
V3 = - 3.31 x 1014/r + 1.32 x 10-7 r2 - 1.6 x 107
(J/kg),
em que a constante adicionada provém da condição
V3(r = RT) = V4(r = RT).
V2 = - 2.18 x 1014/r + 3.92 x 10-7 r2 - 4.4 x 107
(J/kg),
em que a constante adicionada provém da condição
V2(r = 6 x 106 m) = V3(r = 6 x 106 m).
V1 = 2.1 x 10-6 r2 - 1.26 x 108
(J/kg),
em que a constante adicionada provém da condição
V1(r = 4 x 106 m) = V2(r = 4 x 106 m).
|
(4.0) 2) |
Um comboio
com velocidade constante v=30 m/s precorre uma região
em que existe um fortíssimo campo magnético B=20 T (sempre perpendicular
ao chão e orientado de baixo
para cima). Suponha que ligando os carris algures muito à frente do
comboio, está colocada uma barra condutora, de resistência
desprezável (despreze também a resistência eléctrica dos
carris, distanciados entre si de 1 m).
Admita que os eixos das rodas do comboio são todos fracamente condutores,
cada conjunto de 1 eixo e duas rodas com resistência
R=16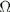 , e
que este comboio é constituído por uma locomotiva automotora
diesel e 3 carruagens, cada uma com 4 eixos. , e
que este comboio é constituído por uma locomotiva automotora
diesel e 3 carruagens, cada uma com 4 eixos.

(1.0) a) Se substituísse todos os eixos do comboio por um único eixo, qual
teria de ser a sua resistência eléctrica equivalente?
Resposta possível:
Todos os eixos estão ligados em paralelo pelos carris, portanto a resistência equivalente é dada por
Req =
1 / (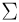 i(1/Ri)) =
1/(16/R) = R/16 = 1 i(1/Ri)) =
1/(16/R) = R/16 = 1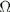
(1.5) b) Qual a variação no tempo do fluxo magnético que atravessa a
área englobada pelo circuito fechado constituído pelos carris, a barra
sobre estes e os eixos do comboio (despreze o comprimento do comboio)?
Resposta possível:
A área englobada pelo circuito [barra condutora fixa + 2 carris + eixo(s) do comboio], num instante t em
que a distāncia do comboio ą barra fixa é X, é dada por lX (l é a distāncia entre os carris = 1 m), e o
fluxo nesse instante, é dado por BlX. A variação no tempo do fluxo do campo
magnético, é dada por
d (BlX) /dt = Bl dX/dt = Blv = 20T.1m.30m/s = 600 Tm2/s = 600 V(volt).
(1.5) c) Qual a intensidade, direcção e sentido da corrente induzida pelo
movimento do comboio nos carris?
Resposta possível:
O fluxo diminui, por isso o sentido da variação do fluxo é contrário ao sentido do próprio fluxo,
isto é, contrário ao sentido de B. A corrente induzida tem de ter um sentido tal
que produza um campo Bind induzido com o mesmo sentido de B.
Pela regra do produto externo (ou da mão direita), o sentido da corrente induzida tem de
ser, no circuito visto de cima (sentido de visão contrário ao de B), o sentido directo
ou contrário ao dos ponteiros do relógio.
O módulo de i é dado pela razão entre a força electromotriz e R, e a primeira é dada pela
variação no tempo do fluxo do campo magnético, calculado na alínea anterior:
i = 600/R = 600 A.
|
|
(4.0/6.0) 3) |
Uma película de Fluoreto de Magnésio, de índice de
refracção n=1.38 e espessura
d=0.1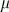 m, cobre uma lente de uma máquina
fotográfica, de índice de refracção nL=1.7.
Considere sempre incidência normal. m, cobre uma lente de uma máquina
fotográfica, de índice de refracção nL=1.7.
Considere sempre incidência normal.
(1.0/1.5) a) Qual o comprimento de onda para o qual a intensidade reflectida
é máxima (primeiro máximo)?
E qual o comprimento de onda para o qual essa intensidade é
mínima (primeiro mínimo)?
Resposta possível:
Ambas as 2 ondas reflectem em meios mais densos (película de MgF2 (=MF)
mais densa do que o ar, e lente mais densa do que MF), portanto ambas são
reflectidas em oposição de fase. A diferença de fase entre elas é devida apenas ą
diferença de percurso, 2nd (sendo d a expessura de MF, e tendo em conta a alteração
do comprimento de onda com o índice de refracção n).
Temos o primeiro máximo de intensidade (m=1), quando houver interferência constructiva, ou que
2nd = m , isto é, quando , isto é, quando
 = 2nd = 276 nm. = 2nd = 276 nm.
Temos o primeiro mínimo de intensidade (m=0) quando
2nd = (m+0.5) <=> <=>
 = 4nd = 552 nm. = 4nd = 552 nm.
(3.0/4.5) b) Cai uma gota de óleo, de índice de refracção n=1.5,
cobrindo uniformente a lente (isto é, que cobre a película sobre a lente).
| (1.5/2.0) i) |
Qual o maior
comprimento de onda que permite obter a
onda reflectida mais intensa (note que será o resultado da soma de
3 ondas reflectidas)? Nestas condições qual a espessura da camada de
óleo? |
| (1.5/2.5) ii) |
Qual o
maior comprimento de onda que permite obter a
onda reflectida menos intensa (resultado da interferência
globalmente destrutiva de 3 ondas - consulte cabeçalho)? |
Possível resposta:
Temos agora a soma de 3 ondas, que interferem globalmente de forma totalmente construtiva
(para um máximo de intensidade), totalmente destructiva (para um mínimo de intensidade),
ou de forma parcialmente constructiva ou destructiva (para uma intensidade variável).
Duas dessas ondas reflectem em meios mais densos, portanto em oposição de fase, e
a terceira reflecte na superfície de separação óleo-MF, e não sofre essa alteração de fase
(pois MF é menos denso do que este óleo).
i) Para obtermos intensidade máxima, todas as ondas têm que chegar em fase! Entre a onda
que reflecte no óleo e a que reflecte na lente, a respectiva diferença de fase deve-se apenas
ą diferença de percurso: 2nol + 2nd
(em que no é o índice de refracção do óleo e l é a espessura do óleo).
Se esta for igual a 1. (m (m com m>1 corresponde a comprimentos de
onda com m>1 corresponde a comprimentos de
onda  menores e pretende-se o maior comprimento de onda), essas duas ondas estarão
em fase, ą chegada ao detector. menores e pretende-se o maior comprimento de onda), essas duas ondas estarão
em fase, ą chegada ao detector.
Entre a onda que reflecte no óleo (que reflecte em oposição de fase) e a que reflecte na MF
(que não sofre alteração de fase na reflexão), a diferença de fase é
 +d.p., em que d.p. é a diferença de fase devido ą diferença de percurso. Para essas duas ondas
chegarem em fase, temos que ter d.p.= +d.p., em que d.p. é a diferença de fase devido ą diferença de percurso. Para essas duas ondas
chegarem em fase, temos que ter d.p.= , que corresponde a uma diferença de percurso de , que corresponde a uma diferença de percurso de
 /2: 2nol = /2: 2nol =  /2.
Temos assim duas incógnitas (l e /2.
Temos assim duas incógnitas (l e  ) e duas equações: 2nol + 2nd = ) e duas equações: 2nol + 2nd =  e 2nol =
e 2nol =  /2. Podemos assim concluir que 2nd = /2. Podemos assim concluir que 2nd =  /2, ou que /2, ou que
 = 4nd = 552 nm, e l = = 4nd = 552 nm, e l =  /(4no) = 92 nm. /(4no) = 92 nm.
ii) Para termos interferência globalmente destructiva, a soma das 3 ondas ą chegada tem que ser
nula! De acordo com o cabeçalho da prova, temos que ter diferenças de fase de
2 /N = 2 /N = 2 /3 entre duas ondas "vizinhas". Como há 3 ondas, há 2 diferentes diferenças de fase:
2 /3 entre duas ondas "vizinhas". Como há 3 ondas, há 2 diferentes diferenças de fase:
2 /3 e 4 /3 e 4 /3. /3.
A onda que reflecte no MF já tem uma diferença de fase em relação a qualquer das outras,
independentemente da respectiva d.p., de  = 3 = 3 /3. Se d.p. desta onda (em relação
ą que reflecte no óleo) for /3. Se d.p. desta onda (em relação
ą que reflecte no óleo) for  /3, então a diferença de fase entre as duas ondas, ą chegada,
será de /3, então a diferença de fase entre as duas ondas, ą chegada,
será de  + + /3 = 4 /3 = 4 /3. Com esta d.p.= /3. Com esta d.p.= /3, podemos escrever /3, podemos escrever
2nol =  /6. /6.
Em relação ao outro par (onda que reflecte na lente em
relação ą onda que reflecte no óleo), basta que a sua d.p.=2 /3, ou que /3, ou que
2nol + 2nd =  /3. /3.
Com as duas equações acima podemos concluir  =12 no l = 1656 nm
(note-se que l já foi determinado e vale 92 nm). =12 no l = 1656 nm
(note-se que l já foi determinado e vale 92 nm).
|
|
(4.0/7.0) 4) |
Num colisionador de muões em estudo, aceleram-se estas partículas
elementares
primas do electrão (em tudo iguais excepto na massa, que
para os muões é m=1.06 x 108 eV/c2, ~= 201 vezes
a massa do electrão), até energias próximas de E=1 TeV (1012 eV).
(1.0/1.5) a) Qual a velocidade aproximada dos muões?
(se não fez esta alínea, assuma nas seguintes o valor v=0.9995c)
Possível resposta:
E2 = m2c4 + P2c2,
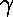 =E/(mc2) = 1/(1- =E/(mc2) = 1/(1-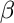 2)1/2, e 2)1/2, e 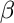 =v/c=cP/E. =v/c=cP/E.
Assim, v = c.(cP/E)=c (E2-m2c4)1/2/E =
0.9999999888 c.
(1.0/2.0) b) Sabendo que a vida média do muão no seu referencial próprio
é 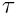 =2.2
=2.2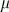 s, quanto
tempo duram esses muões no acelerador, em média? s, quanto
tempo duram esses muões no acelerador, em média?
Possível resposta:
A vida média no refencial próprio dos muões, 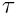 ,
é medida na Terra como o tempo ,
é medida na Terra como o tempo
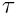 T = T = 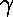
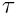 .
Com .
Com 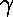 =E/(mc2) = 9434, =E/(mc2) = 9434,
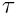 T = 20.75 ms. T = 20.75 ms.
(1.0/2.0) c) Se no acelerador medíssemos o tamanho dos muões como sendo
d=10-18 m, qual seria o tamanho respectivo no seu referencial
próprio?
Para uma distāncia d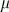 medida no referencial próprio dos muões, mede-se
uma distāncia na terra dada por : medida no referencial próprio dos muões, mede-se
uma distāncia na terra dada por :
dT = d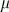 / /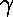 = 10-18 m. <=>
d = 10-18 m. <=>
d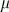 = 9.4 x 10d-15 m = 9.4 x 10d-15 m
(1.0/1.5) d) Se um muão destes falasse com frequência da onda sonora f=500
Hz, conseguiríamos nós ouvi-lo quando se dirigisse para nós
(justifique)? Se sim, com que frequência?
Resposta possível:
Enquanto se dirige para nós, o muão aproxima-se com uma velocidade próxima de c, portanto muito
superior ą velocidade das ondas sonoras por ele emitidas, 344 m/s. Portanto o muão
chega antes de qualquer onda sonora por ele emitida <=> antes dele chegar, também não
chega nenhuma onda sonora <=>
Não o conseguiríamos ouvir!
|
|
(4.0/7.0) 5) |
Um laser de luz laranja emite num comprimento de onda aproximadamente igual a
600~nm. Considere um modelo para o laser em que os fotões são emitidos
devido a transições de electrões entre os níveis de energia n=2 e n=3,
numa caixa de paredes infinitas.
(1.0/1.0) a) Se um estudante da L.E.G.I. se aproximar deste laser no seu
Berrari recentemente oferecido e observar luz azul
( =450 nm), qual a sua velocidade? =450 nm), qual a sua velocidade?
Resposta possível:
O comprimento de onda da onda luminosa recebida pelo estudante
enquanto se aproxima da fonte,
 ', é dado pelo
efeito Döppler relativista aplicado ao comprimento de onda da
onda emitida, ', é dado pelo
efeito Döppler relativista aplicado ao comprimento de onda da
onda emitida,  : :
 ' = ' =  ( (c - v)/(c + v) )1/2 <=>
(450 nm)2 = 6002 (c - v)/(c + v) <=>
v = c (6002 + 4502)/(6002 + 4502) = 0.28 c ( (c - v)/(c + v) )1/2 <=>
(450 nm)2 = 6002 (c - v)/(c + v) <=>
v = c (6002 + 4502)/(6002 + 4502) = 0.28 c
(muito superior ao limite legal em autoestrada de 120 Km/h)!
(1.5/3.0) b) Qual a diferença de energia entre os níveis referidos?
Resposta possível:
Corresponde ą energia do fotão emitido pelo laser = E = hf = hc/ = 3.31 x 10-19 J = 2.06 eV. = 3.31 x 10-19 J = 2.06 eV.
(1.5/3.0) c) Qual a largura da caixa que é compatível com este laser?
(sugestão: dentro da caixa, onde os electrões estão confinados,
a função potencial U é nula! Pense na relação entre
energia e momento (desprezando a relatividade), entre este e o
comprimento de onda, e finalmente pense nos comprimentos de onda
possíveis para uma caixa de largura a)
Resposta possível:
O modelo da caixa de paredes infinitas, obriga a função de onda do electrão a anular-se
nos extremos da caixa de largura a, ou seja (analogia para uma corda estacionária
de comprimento a), os seus comprimentos de onda possíveis respeitam a relação:
n e = 2 a <=> e = 2 a <=>  e = 2a/n e = 2a/n
Por outro lado,  e = h/P, e E=P2/2m + U. Como dentro
desta caixa os electrões estão livres (U=0), vem e = h/P, e E=P2/2m + U. Como dentro
desta caixa os electrões estão livres (U=0), vem
En= Pn2 /2m =
h2/(2m n2) =
h2/(2m (2a/n)2 ) =
n2h2 / (8m a2). n2) =
h2/(2m (2a/n)2 ) =
n2h2 / (8m a2).
Assim, E3 - E2 =
32 h2 / (8m a2) -
22 h2 / (8m a2) = 5 h2 / (8m a2) =
3.31 x 10-19 J (calculado na alínea anterior).
Assim, a = ( 5h2 / (8m . 3.31 x 10-19 J ) ) = 9.54 x 10-10 m.
|


