9ª Série de Problemas

Mecânica e Ondas

LEEC/LEE/LEGI

1. A frequência característica de uma massa presa a uma mola é de 5 Hz.

a) Qual a aceleração da massa quando o deslocamento é de 0.51 m?

b) Porque factor se devia aumentar a massa para duplicar o período da oscilação?

2. A Fig. representa um pêndulo cujo ponto de suspensão se move sem atrito sobre uma linha recta; a massa do bloco onde o pêndulo está suspenso é desprezável em relação a m e o fio é inextensível (m=1 kg e l=1 m).

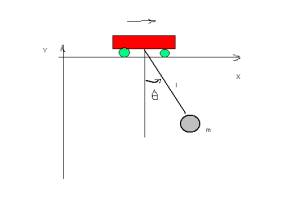
a) Supondo que o movimento do bloco onde o pêndulo está suspenso é descrito por uma função b(t) conhecida, quantos graus de liberdade tem o sistema? Escreva o lagrangeano e as equações do movimento.

b) Particularize para b(t)=at²/2, com a=2 m.s^-2 (ponto de suspensão movendo-se com aceleração constante). Determine o ponto de equilíbrio e resolva a equação do movimento para pequenas oscilações.

c) Particularize para b(t)=2 cos 3t (ponto de suspensão oscilando no tempo) e resolva a equação do movimento para pequenas oscilações.

d) Particularize para b(t)=2 cos 4t e resolva a equação do movimento para pequenas oscilações. Compare este caso e o da alínea anterior. Esboce como varia a amplitude e o desfasamento em função dos parâmetros do sistema e da frequência exterior.

3. Qual a contracção do diâmetro da Terra para um astronauta que se encontre em repouso relativamente ao Sol? (considere a Terra como um referencial de inércia num pequeno intervalo de tempo). A velocidade orbital da Terra relativa ao Sol é de 30 km/s e o raio da Terra é de 6.37 x 10⁶ m

4. A vida média de uma partícula é 100 ns no seu referencial próprio.

4.a) Qual a duração da partícula no laboratório, sabendo que a sua velocidade é de 0.960c ?

4.b)Quanto mede o percurso da partícula no laboratório durante a sua existência?

4.c) Quanto mediria o mesmo percurso se o tempo fosse igual no laboratório e no referencial próprio da partícula, como na Física Clássica.

5. Uma nave espacial tem comprimento L=300 m. Imagine que o seu coman-dante está no centro da nave enviando simultaneamente dois feixes de luz, um para cada lado oposto da nave onde actuam um mecanismo de abertura automática de portas.

5.a) Calcule o instante em que a luz atinge a parede do lado esquerdo. A nave espacial relativista move-se da esquerda para a direita com velocidade v=0.8c relativamente ao espaçoporto (estação espacial).

5.b) Calcule, no referencial da nave, ao fim de quanto tempo abrem as portas da frente e a de trás, situadas nos dois extremos opostos da nave. A abertura das portas é simultânea no ponto de vista do capitão?

5.c) Refaça a alínea 5.a) no referencial do espaçoporto.

6. Um neutrão livre tem um período de semi-vida no seu referencial próprio de 11.0 min. (só no núcleo, com outros neutrões e protões, é que o neutrão é mais estável), desintegrando-se num electrão, num protão e num neutrino (declínio b-). Considere um feixe de neutrões produzido numa das muitas reacções de fusão nuclear que ocorrem no Sol.

6.a) Quanto tempo deve decorrer no referencial próprio dos neutrões para que o seu número se reduza a 1% do número inicial? (Lembre-se do declínio radioactivo)

6.b) Suponha que os neutrões se deslocam a uma velocidade média de 10⁶ m/s (na realidade a velocidade é menor) e considere que a distância Terra-Sol é de 1.49 x 10¹¹ m. Quanto tempo demoraria um neutrão a chegar à Terra, para um observador na Terra?

6.c) A partir dos resultados de a) e de b), diga se há perigo de os neutrões solares atingirem a Terra. (Lembre-se que só pode comparar grandezas medidas no mesmo referencial!).